Τυπική Απόκλιση Δειγμάτων

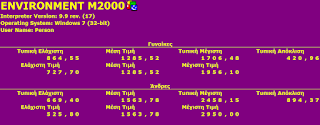
Το παράδειγμα από εδώ έγινε προγραμματιστικά με την Μ2000. Με λίγα λόγια δίνουμε δυο σειρές δεδομένων, και μας επιστρέφουν τιμές όπως ελάχιστη, μέση, μέγιστη, τυπική απόκλιση, τυπική ελάχιστη (ως διαφορά μέσης με τυπική απόκλιση), και τυπική μέγιστη (ως  άθροισμα μέσης και τυπικής απόκλισης)

Τοι πρόγραμμα το γράφουμε σε ένα τμήμα έστω Α (Σ Α enter και αντιγράφουμε, μετά πατάμε το Esc και επιστρέφουμε στην γραμμή εντολών και γράφουμε Α enter και έτσι το εκτελούμε)

Περιλαμβάνει μια συνάρτηση που δίνει τέσσερα νούμερα ενώ δέχεται ένα δείκτη σε πίνακα δειγμάτων (αριθμητικών τιμών). Δίνει λάθος αν δεν υπάρχουν τουλάχιστον δυο στοιχεία.
Επίσης υπάρχει και μια ρουτίνα που κάνει την όλη εργασία για κάθε σύνολο τιμών. Δέχεται δυο δεδομένα, την επιγραφή και το πίνακα δειγμάτων.

Εξ ορισμού μια τιμή 1 είναι τύπου double, δεν χρειάζεται να βάλουμε το 1.0 τιμές άλλων τύπων έχουν χαρακτήρες όπως πχ το # για τιμή τύπου λογιστικό (Currency) έτσι το 10.45# είναι λογιστικό.

Το ΔΙΑ είναι η ακέραια διαίρεση, όχι ειδικά για ακέραιους, και επιστρέφει τιμή
πχ το μ είναι Single (αν είχαμε δώσει 10~ δια 2 θα ήταν double, αλλά τώρα και οι δυο αριθμοί είναι single). Οι συγκρίσεις γυρίζουν boolean, και εδώ συγκρίνουμε έναν single με έναν double.
μ=10~ δια 2~
Τύπωσε  Τύπος$(μ)="Single", μ=5

Επίσης το ΔΙΑ στο 10 ΔΙΑ 2.5 δίνει 4, όπως και στο 11 ΔΙΑ 2.5 δίνει 4 και το 11 ΥΠΟΛ 2.5 δίνει 1.
,
Το Μήκος(Δείκτης) δίνει τον αριθμό στοιχείων του πίνακα που δείχνει ο Δείκτης (τον βλέπει ως μιας διάστασης ακόμα και αν είχε περισσότερες ή γυρίζει 0 αν δεν έχει κανένα στοιχείο)

Η Δείγμα#Αθρ() βγάζει άμεσα το άθροισμα όλων των στοιχείων στο πίνακα.
Το κ=Κάθε(Δείγμα) φτιάχνει το κ ως απαριθμητής του πίνακα που δείχνει η μεταβλητή Δείγμα. Για να λειτουργήσει η κ πρέπει να μπει σε μια Ενώ. Όταν φθάσει στο τέλος απαρίθμησης δίνει ψευδές οπότε η Ενώ τερματίζει (όπως η ΟΣΟ στη ΓΛΩΣΣΑ του σχολείου). Μπορούμε με το κ^ να πάρουμε το νούμερο απαρίθμησης (το κ είναι αντικείμενο οπότε το ^ εδώ δεν είναι η ύψωση σε δύναμη, αλλά τελεστής του αντικειμένου). Εδώ θα πάρουμε την τιμή με την Πίνακας(α). Η Πίνακας(Δείγμα) δίνει το πρώτο (στοιχείο στο  0) ενώ το Πίνακας(Δείγμα, 1) δίνει το 1, αλλά η Πίνακας() όταν βλέπει ότι έχει να κάνει με απαριθμητή πίνακα παίρνει το νούμερο από τον απαριθμητή. Δείτε στην ρουτίνα πιο κάτω ότι το ΑΠ που είναι δείκτης σε πίνακα όπως το Δείκτης. Εκεί το ΑΠ#Τιμή(0) είναι το ίδιο με το Πίνακας(ΑΠ) ενώ το ΑΠ#Τιμή(1) είναι το Πίνακας(ΑΠ,1). Και για τιμές αλφαριθμητικών έχουμε τα αντίστοιχα #Τιμή$() και Πίνακας$().

\\ Τυπική απόκλιση δειγμάτων
\\ Δίνουμε ένα δείκτη σε πίνακα (tuple)
\\ Λαμβάνουμε έναν άλλο δείκτη σε πίνακα (τις απαντήσεις)
\\ Η συνάρτηση έχει δικό της όνομα χώρου, έτσι οι μεταβλητές που ορίζουμε
\\ δεν μπλέκονται με άλλες εκτός συνάρτησης
\\ Η συνάρτηση πρέπει να οριστεί πριν την χρήση της
\\ αυτό συμβαίνει γιατί η Μ2000 είναι δυναμική γλώσσα, έτσι ώστε
\\ για να υπάρχει μια συνάρτηση πρέπει να εκτελεστεί ο ορισμός της.
\\ Αυτό σημαίνει ότι μπορούμε να επιλέγουμε ορισμούς δυναμικά.
\\ Το ίδιο γίνεται και με τα τμήματα.
\\ Τα τμήματα δεν γυρίζουν τιμές σε εκφράσεις αλλά χειρίζονται τον σωρό τιμών
\\ έτσι μπορούν να βάλουν τιμές σε αυτόν ως επιστροφή
\\ Οι ρουτίνες διαφέρουν γιατί δεν μπορούν να αλλάξουν δυναμικά.
\\ Έχουν μόνο έναν ορισμό και  για το λόγο αυτό βρίσκονται στο τέλος του τμήματος
\\ ή της συνάρτησης που ανήκουν.
\\ Επιπλέον μια ρουτίνα βλέπει ότι υπάρχει στο τμήμα, και τον εαυτό της.
\\ Οι τυπικές παράμετροι της ρουτίνας σκιάζουν οποιεσδήποτε μεταβλητές με το ίδιο όνομα
\\ Εδώ φτιάχνουμε μια επιπλέον τοπική το ΠΛ. Όταν η ρουτίνα τερματίσει οι τυπικές παράμετροι και το ΠΛ θα σβηστούν.
\\ Ο σωρός τιμών όπως και στα τμήματα έτσι και στις ρουτίνες δίνεται ως έχει και είναι θέμα της ρουτίνας για το  πώς θα τον πειράξει. Εδώ "σηκώνουμε" δυο μεταβλητές (ως τυπικές παραμέτρους).


Συνάρτηση Υπολογισμός_Τυπικής_Απόκλισης (Δείγμα) {
      Αν Μήκος(Δείγμα)<2 τότε Λάθος "Αριθμός δειγμάτων μικρότερος του 2"
      Μέσος_Όρος=Δείγμα#Αθρ()/Μήκος(Δείγμα)
      Τ_Απόκλιση=0
      κ=κάθε(Δείγμα)
      Ενώ κ {
            Τ_Απόκλιση+=(Πίνακας(κ)-Μέσος_Όρος)**2
      }
      Τ_Απόκλιση/=Μήκος(Δείγμα)-1
      Τ_Απόκλιση=Ρίζα(Τ_Απόκλιση)
      =Τ_Απόκλιση,Μέσος_Όρος, Δείγμα#Μικ(), Δείγμα#Μεγ()
}


\\ η απαρίθμηση είναι σταθερές με μια "συνέχεια" προηγούμενου-επόμενου
\\ εδώ λειτουργούν απλά σαν σταθερές με τιμές 0,1,2,3
\\ και τις βάζουμε στον πίνακα που μας επιστρέφει η συνάρτηση
\\ Υπολογισμός_Τυπικής_Απόκλισης()


Απαρ Τιμές {Απόκλιση=0, Μέση, Ελάχιστη, Μέγιστη}


\\ αρχικά αδειάζουμε το σωρό τιμών
Άδειασε
\\ χρήση σωρού τιμών ως FIFO
\\ Βάζουμε τέσσερα πράγματα, αλφαριθμητικό, δείκτης σε πίνακα, αλφαριθμητικό, δείκτης σε πίνακα
Σειρά "Γυναίκες", (727.7, 1086.5, 1091, 1361.3,1490.5,1956.1)
Σειρά "Άνδρες", (525.8, 605.7, 843.3, 1195.5, 1945.6, 2135.6, 2308.7, 2950.0)
Σημ Σωρός \\ δείχνει τι έχει ο σωρός, στους πίνακες δίνει το *[mArray] όπου το * λέει δείκτης, και το mArray είναι το αντικείμενο πίνακας. Βγάλτε το Σημ η πατήστε ένα enter ώστε να κατέβει γραμμή η Σωρός.


\\ όσο ο σωρός δεν είναι κενός θα καλούμε το ΔείξεΤιμές()
Ενώ όχι κενό
    ΔείξεΤιμές() ' ήδη είναι στο σωρό τιμών τα δεδομένα
Τέλος Ενώ
Τέλος


Ρουτίνα ΔείξεΤιμές(Κειμ$, Απ)
    Απ=Υπολογισμός_Τυπικής_Απόκλισης(Απ)
    \\ χωρίζουμε την οθόνη σε τέσσερις στήλες
    Τοπική Πλ=Πλάτος Δια 4
    Τύπωσε Πάνω $(6), Κειμ$ ' κεντραρισμένο σε όλο το πλάτος
    Τύπωσε Υπό ' υπογράμμιση
    \\ κεντραρισμένοι τίτλοι στις στήλες με αναλογική γραφή
    Τύπωσε $(6,ΠΛ),"Τυπική Ελάχιστη","Μέση Τιμή", "Τυπική Μέγιστη","Τυπική Απόκλιση"
    Τύπωσε $("#.00"),$(0),Απ#Τιμή(Μέση)-Απ#Τιμή(Απόκλιση), Απ#Τιμή(Μέση), Απ#Τιμή(Μέση)+Απ#Τιμή(Απόκλιση), Απ#Τιμή(Απόκλιση)
    Τύπωσε $(6), "Ελάχιστη Τιμή","Μέση Τιμή","Μέγιστη Τιμή"
    \\ επαναφέρουμε τη στρογγύλευση στο αρχικό με το $("") και το απαραίτητο διπλό κόμα.
    Τύπωσε $(0),Απ#Τιμή(Ελάχιστη), Απ#Τιμή(Μέση), Απ#Τιμή(Μέγιστη)
    Τύπωσε $("")
    Τύπωσε
Τέλος Ρουτίνας

Revision 17, Version 9.9

From revision 18 change the file. slight. Instead of use of "'" now use "!" for accurate search operation.  Inside info there is a module name MAKEHELP with the updated version.
Also there is an EXPORTHELPNEW which export Greek or English help (ask to press G pr E). First import to a 2D array and make a sort on columns using first key on groups and second key on identifiers.

The mEditor in Info which is a GUI editor for M2000 programs, use two EditBoxes, one for editing the code and another for viewing topics from help.So the program updated to use either of help files, mdb and dat (the dat file is a text file in UTF8 format, where the memo field is one line using escape codes like \c\n for CRLF)


New Help File. (Not used any more, see above)

 greek$="\"+ALL(i)#val$(0)+"'"+str$(ALL(i)#val(3),"")+

 english$="\"+ALL(i)#val$(2)+"'"+str$(ALL(i)#val(3),"")+

change to that (check the ! char)

 greek$="\"+ALL(i)#val$(0)+"!"+str$(ALL(i)#val(3),"")+

 english$="\"+ALL(i)#val$(2)+"!"+str$(ALL(i)#val(3),"")+

We can use the mdb (Access 2007 file)  using switch "+mdb". By default now Interpreter use a dat file, A utf8 file including all help base, only for reading.

We can make the dat file from mdb using this program. To work this program we have to copy Help2000.mdb ro user folder (open with the statement Win Dir$) We get the export to the same folder


Module MakeHelp {

 pen 14 : cls 5
 flush
 \\DIR APPDIR$ \\  from installation folder use this
 Retrieve "HELP2000","GROUP", 1,"",""
 Read many
 Flush
 Dim Labels$(1 to 25), ser(1 to many)
 For i=1 to many
 Retrieve "HELP2000","GROUP", i,"",""
 drop
 Read where, Labels$(where)
 ser(i)=where
 flush
 next i
 Retrieve  "HELP2000", "SELECT * FROM COMMANDS",1,"",""
 Read many
 dim ALL(1 to many)
 Document infoGr$, Info$, greek$, english$
 br$={__<ENG>__
 }
 nl$=string$({
 } as json )
 p1=1
 for i=1 to many
 Retrieve  "HELP2000", "SELECT * FROM COMMANDS",i,"",""
 drop
 ALL(i)=Array([])
 Print ALL(i)#val$(2), rightpart$(Labels$(ALL(i)#val(3)), ","+chr$(160))
 Print ALL(i)#val$(0), leftpart$(Labels$(ALL(i)#val(3)), ","+chr$(160))
 greek$="\"+ALL(i)#val$(0)+"'"+str$(ALL(i)#val(3),"")+{
 }
 english$="\"+ALL(i)#val$(2)+"'"+str$(ALL(i)#val(3),"")+"-"+Str$(i)
 if i<many then
  english$={
  }
 end if
 infoone$="GR:"+ALL(i)#val$(0)+nl$+string$(rightpart$(ALL(i)#val$(1), br$) as json)
 info$=infoone$+{
 }
 infoone$="EN:"+ALL(i)#val$(2)+nl$+string$(leftpart$(ALL(i)#val$(1), br$) as json)
 infoGR$=infoone$+{
 }
 next
 Method english$, "SetLocaleCompare", 1033
 Method english$, "SetBinaryCompare"
 Sort english$
 Dir User   \\ open this using Win Dir$
 open "Help2000.dat" for wide output as #k
 Print #k, Len(Labels$())
 for i=1 to len(Labels$())
  Print #k, Labels$(i)
 next i
 Print #k, Many
 Print #k, infoGr$;info$;greek$;english$
 close #k
 clear
 Document ALL$, all1$
 Load.doc ALL$, "help2000.dat"
 print filelen("help2000.dat")
 save.doc all$,"help2000utf8.dat", 2   ' utf-9
 print filelen("help2000utf8.dat")
}
MakeHelp

We can also read the file using M2000 code

also here change

   Print leftpart$(Ret$,"'")
   lbl=Val(Rightpart$(Ret$,"'"))

to

   Print leftpart$(Ret$,"!")
   lbl=Val(Rightpart$(Ret$,"!"))

The search is serial but very fast. We can find with little letters. eg THR  return THREAD. We can use it for Greek and English identifiers. Write ALL to get all the identifiers.

Module ReadHelp {
 flush
 Document ALL$
 Load.doc ALL$, "help2000utf8.dat"
 A=Val(paragraph$(ALL$, 1))
 B=Val(paragraph$(ALL$, 2+A))
 Find ALL$, paragraph$(ALL$,2+A+1+2*B)
 Read where, no_par, bb
 Find ALL$, paragraph$(ALL$,2+A+1+3*B), where
 drop : read no_par2
 flush
 do
  Input "give a name OR - TO EXIT:", aName$
  if aName$="-" then exit
  if aName$="" then continue
  Find ALL$, "\"+ucase$(aName$), where
  Read Where1
  if Where1>0 then
   read  There : drop
   Ret$=mid$( Paragraph$(ALL$, There), 2)
   Print Ret$
   Print leftpart$(Ret$,"'")
   lbl=Val(Rightpart$(Ret$,"'"))
   info=Val(Rightpart$(Ret$,"-"))
   if info=0 then
    Print lbl
    Print LeftPart$(Paragraph$(All$,lbl+1), ", ")
    Report format$(paragraph$(ALL$,2+A+1+There-no_par))
   else
    Print lbl, info
    Print RightPart$(Paragraph$(All$,lbl+1), ", ")
    Report format$(paragraph$(ALL$,2+A+B+info))
   end if
  end if
  flush
 Always
}
ReadHelp

Installation file now has this file help2000utf8.dat and not Help2000.mdb. You can find mdb file in Github here https://github.com/M2000Interpreter/Version9/blob/master/help2000.mdb

Revsion 16, Version 9.9

1, A serious bug in Sort() function for tuple removed.
2. Another bug in For object {} structure also removed
3. Some light optimizations.
4. Updated Info.gsb. Added PHILO (Dining Philoshophers, an example using threads), and  COLUMNSSORT (Example for sorting 2D arrays for a range of rows using series of columns as keys and choosing ascending or descending type for each key a different one)
5. Updated M2000paper.pdf
6. Installation file M2000language.exe now make a group M2000 in programs, with M2000 for the interpreter, Documentation (shiw M2000paper.pdf) and Readme.(show Readme.txt). So the M2000language.exe install the M2000paper.pdf (zipped together with all parts of the language, like m2000.exe and m2000.dll and the help2000.mdb)

M2000language.exe can be found in Dropbox (see the links in the right top column - in tablet change view to desktop to see the columns)

Or open Μ2000paper.pdf  the same as the one in M2000language.exe

Revision 15, Version 9.9

In this revision

1. A minor fix for Main.Task structure
2. A new installation file with M2000paper.pdf. This is in Github with source code and also is in M2000language.exe so when you install the environment you have in start menu a folder with Documentation (this paper) and M2000 (the m2000.exe)

The M2000 paper is a 200+ pages for M2000 language for learning the basics of the language.

Revision 14, Version 9.9

A bug which crach the M2000 environment at last removed.

See the case on the previous revisions:::
Run m2000.exe
Write Help All   (supposed you have installed the Access2007 runtime)
Write Edit a
Write anything in the module a and press Esc
now close the Help form
Write new
You get the crash, because the new statement check that you have changes on modules and try to open the msgbox and this give a crash

The same can be done when you load a program, make some changes and then press ctrl+A to save it, if you use help before.

So the solution found to be the loading/unloading the M2000 msgbox form  (hidden from user) at the intitialization stage.

Αναθεώρηση 11, Έκδοση 9.9

Σε αυτήν την έκδοση διορθώθηκε ένα αντικείμενο Mutex ή Μοναδικό το οποίο κρατέι μια λίστα μοναδικών αντικειμένων στο λειτουργικό σύστημα, όπου μόνο ένα πρόγραμμα μπορεί να έχει την ιδιοκτησία του. Με αυτό το τρόπο στο παρεχόμενο info.gsb (στο αρχείο εγκατάστασης) υπάρχει το CLOCK το οποίο ελέγχει αν τρέχει ένα ρολόι με χρήση mutex, και αν ήδη τρέχει τότε το πρόγραμμα (Το τμήμα δηλαδή Clock) τερματίζει (για να μην τρέξει και δεύτερη φορά). Όταν γράφουμε CLOCK εκτελείται το CLOCK1 το οποίο ανοίγει δεύτερο m2000.exe και κάνει τα μαγικά του για να τρέξει εκεί το CLOCK (και εκεί κοιτάει αν ήδη τρέχει οπότε τερματίζει πριν μας δείξει το ρολόι).

Επίσης μπήκε κώδικας που επιστρέφει λάθος όταν περάσουμε με αναφορά μια στατική μεταβλητή ή ένα στοιχείο πίνακα σε ρουτίνα. Κανονικά μόνο σε κλήση τμήματος και συνάρτηση μπορούν να γίνουν αυτά τα περάσματα με αναφορά, γιατί λειτουργούν με copy in copy out, και ο μηχανισμός συνδέεται με το αντικείμενο εκτέλεσης το οποίο έχουν τα τμήματα και οι συναρτήσεις αλλά δεν έχουν οι ρουτίνες (οι οποίες μοιράζονται το αντικείμενο εκτέλεσης στο περιβάλλον που καλούνται).

Στο info.gsb μπήκε και το OOP2, που δείχνει ότι το OOP1 δηλαδή πως φτιάχνουμε με προγραμματισμό με αντικείμενα υποδομή για γεγονότα (το OOP1 είχα φτιάξει πριν φτιάξω το αντικείμενο Γεγονός και ότι άλλο έφερε μετά αυτό, όπως το γραφικό σύστημα διεπαφής χρήστη GUI). Στο OOP2 αλλάζουμε το σχεδιασμό των αντικειμένων ώστε να έχουμε ένα κοινό αντικείμενο το οποίο να κληρονομεί άλλα δύο (όπου στο OOP1 τα δυο αυτά δεν έχουν κοινό πρόγονο, αλλά έχουν ακριβώς την ίδια χρήση, με ίδιο σχεδιασμό στο 90% χοντρικά θα λέγαμε).

Μπήκε το Conv2 το πρόγραμμα για την μετατροπή βάσης.

Ανέβηκε μια πιο βελτιωμένη έκδοση του μικρού εγχειριδίου (με ημερομηνία 21/3/2020). Μπήκαν νέα παραδείγματα και μια επεξήγηση για τα περάσματα με αναφορά,.
Ένα από τα παραδείγματα είναι το Textout στα ελληνικά. Το πρόγραμμα στα αγγλικά υπάρχει στο info.gsb και δείχνει πως δείχνουμε κείμενο ενώ ταυτόχρονα το προφέρει το σύστημα ομιλίας.

Αυτή την εποχή έχω χρόνο (είμαι ήδη μια εβδομάδα μέσα στο σπίτι λόγω της επιδημίας του κορονοϊού)

Επιπλέον γράφω ένα paper στα Αγγλικά για να εξηγεί με παραδείγματα τη γλώσσα Μ2000 (όχι το περιβάλλον) στη βασική της μορφή, τα στοιχεία της γλώσσας, και το πως προγραμματίζουμε με το παλιό στυλ και πως με το νέο, και φυσικά ορίζω τι είναι παλιό και τι νέο. Είναι τώρα 41 σελίδες και ελπίζω να μην περάσει τις 80. Κάποια στιγμή θα το φτιάξω και στα Ελληνικά. Είναι διαφορετικό από το Μικρό Εγχειρίδιο. Στο Μικρό εγχειρίδιο γίνεται αναφορά στη Γλώσσα Μ2000 και στο Περιβάλλον Μ2000, με τεχνικές λεπτομέρειες, και ομαδοποιημένα με στόχο να λειτουργεί σαν σημείο αναφοράς. Το paper είναι για εκπαίδευση, χωρίς όμως ασκήσεις.δηλαδή αναφέρεται σε μικρά προγράμματα και παράλληλα δείχνει τα στοιχεία της γλώσσας.

Λόγω καραντίνας λοιπόν θα υπάρξει χρόνος να ασχοληθεί κανείς με την Μ2000.

Καλή Καραντίνα σε όλους

Base Conversion an Example

First publish here in Rosettacode.org

The code is very compact. We use here ** for power (also ^ can be used for power).
M2000 is like Basic, but with advance constructions like lambda functions. Each lambda function return not a lambda but the result of a new lambda (see the immediate call using (m) and (m$) after the block {} in each lambda. The closures z$ and b are there for each recursive call.

Module Checkit {
 k$=lambda$ (m, b as integer=16) -> {
  if b<2 or b>16 then error "base out of range"
  if m=0 then ="0" : exit
  z$="0123456789ABCDEF" 
  =lambda$ z$, b (m) ->{
   =if$(m=0->"", lambda$(m div b)+mid$(z$, m mod b + 1, 1))
  }(m)
 }
 k=lambda (m$, b as integer=16) -> {
  if b<2 or b>16 then error "base out of range"
  m$=trim$(m$)
  if m$="0" then =0 : exit
  z$="0123456789ABCDEF" 
  =lambda z$, b (m$) ->{
   =if(Len(m$)=0->0, lambda(mid$(m$,2))+(instr(z$, left$(m$,1))-1)*b**(len(m$)-1))
  }(m$)
 }
 Print k$(0)="0", k("0")=0
 Print k$(65535)="FFFF", k("FFFF", 16)=65535
 Print k$(0xF00F)="F00F", k("F00F", 16)=0xF00F
 Print k$(0xFFFFFFFF)="FFFFFFFF", k("FFFFFFFF", 16)=0xFFFFFFFF
 Print k$(100, 8)="144", k("144", 8)=100
 Print k$(100, 2)="1100100", k("1100100", 2)=100
}
Checkit

Open a form after closing from unload button

This is an example of how we use a form, here with a handler as SIMPLE, to pass it to three modules, Inner, Inner1 and Inner2. Each module open the form, and when we close it using the unload button on the header of the form we make a fake unload using the Unload event, which handle the visible property to hide the form.

The Inner module get a copy of the window handler. This copy can't be used to make a linked property.

Why that happen ? Is the way M2000 interpreter internal window manager work. Only one real reference to a form exist. This means that when the module CheckIt exit, this reference released, and the form unloaded. The same done when we place a Nothing. When we click on unload button, an unload happen except we cancel it using the true as value to the first by reference variable at unload event. All events called in the same module we make the form and they have the name of the declaration, here the SIMPLE, here the simple.unload function is the service routine for the event. The call is a local type, which means that inside code in function Sumple.Unload we have the visibility of module checkit, so we can see the visible property.

So in Inner module we open the form as modal, using the m2000 internal window manager for modal windows. When we click on unload button, the modal loop exit, but the form not unload, but hide.

When we call the Inner1 we pass the Simple by reference, so we can make a visible property. Now we use a simple loop on visible property to make it like a modal (but a modal type to show also lock the under the form forms).

When we call the Inner2 we pass the Simple and the Visible both by reference.

Although the name of form inside Inner, Inner1 and Inner2 is That, the actual form has the name Simple and a prefix, as a weak reference to use it to call events. Also has a list for those events that aren't servising. This list erased and make it again if the form loose the focus.

If we make a fault in code, the module's stop working and all the variables erased, so the form unload, because the form's handler always is one. The visible property never hold a reference to form, but a reference to where Simple reference, the real reference which is only one.


Module CheckIt {
      \\ Simple is a first class object
      Declare Simple Form
      \\ we can define form before open
      Layer Simple {
            \\ center Window with 12pt font, 12000 twips width and 6000 twips height
            \\ ; at the end command to center the form in current screen
            Window 12, 12000, 6000;
            \\ make layer gray and split screen 0
            Cls #333333, 0
            \\   set split screen to 3rd line, like Cls ,2 without clear screen
            Scroll Split 2
            Cursor 0, 2
      }
      With Simple, "Title", "Hello Form", "visible" as visible
      \\ Without handling the unload event, a form unload for good
      \\ So we have to cancel the unload event and make the form non visible
      Function Simple.Unload {
            Read New &cancel
            visible=False
            cancel=true
      }
      Function Simple.Click {
            Layer Simple {
                  \\ open msgbox
                  Print Ask("Hello World")
                  Refresh
            }
      }
      Module Inner (That) {
            \\ open as modal  - also we handle the Unload event
            Method That, "Show", 1
      }
      Module Inner1 (&That) {
            \\ we can produce a linked property if we pass by reference
            \\ so &That make That same as Simple
            \\ if we pass by value we get an error "Can't Get Property"
            With That, "visible" as visible
            Method That, "Show"
            do
                  wait 1
            until not visible
      }
      Module Inner2 (&That, &thatToo) {
            Method That, "Show"
            do
                  wait 1
            until not thatToo
      }
      Inner Simple
      wait 1000
      Print "ok"

      Refresh
      Inner1 &Simple
      wait 1000
      Print "ok"

      Refresh
      Inner2 &Simple, &visible
      \\ now form deleted
      \\ Make the Simple as Nothing the form unloaded if not unloaded,
      \\ without an unload event.
      Declare Simple Nothing
}
CheckIt

Δένδρο του Πυθαγόρα (Αναδρομή)

Ένα πρόγραμμα που δείχνει πως λειτουργεί η αναδρομή με τον αλγόριθμο που φτιάχνει το δένδρο του Πυθαγόρα. Κάθε τετράγωνο αν δεν είναι φύλλο έχει άλλα δυο τετράγωνα μικρότερα που σχηματίζουν τρίγωνο στη μια πλευρά του.

Οι ρουτίνες βλέπουν ότι υπάρχει σε ένα τμήμα, ακόμα και το όνομά τους, και έτσι μπορούν να το καλέσουν. Οι παράμετροι και οι τοπικές μεταβλητές με το πέρας εκτέλεσης μιας ρουτίνας διαγράφονται. Αν έχουμε καλέσει τη ρουτίνα του παραδείγματος σε βάθος έστω τρεις κλήσεις τότε πριν την πρώτη Χάραξε θα υπάρχουν στην μνήμη του διερμηνευτή όλες οι προηγούμενες τοπικές μεταβλητές (και οι παράμετροι της ρουτίνας που είναι επίσης τοπικές μεταβλητές, και εξ ορισμού οι κλήσεις στη Μ2000 γίνονται με πέρασμα με τιμή).

Για να πετύχει η αναδρομή χρειάζεται μια συνθήκη εξόδου. Η έξοδος πρέπει να γίνει πριν κληθεί ξανά η ίδια ρουτίνα. Η συνθήκη εδώ είναι ο έλεγχος της τάξης δένδρου, με νούμερο 6, δηλαδή φτιάχνει 6 δένδρα (βάση τετράγωνο, πλευρές μικρά τετράγωνα), όπου το καθένα εκτός από το πρώτο έχει το προηγούμενο ως βάση!

Για την εμφάνιση του δένδρου χρησιμοποιούμε δυο εντολές, την Θέση που δέχεται απόλυτη τιμή καρτεσιανών συντεταγμένων (η πάνω αριστερή γωνία είναι το 0,0 και το ύψος αυξάνει προς τα κάτω οπότε η κάτω δεξιά γωνία είναι η χ.σημεία-πλάτος.σημείου, υ.σημεία-ύψος.σημείου). Οι μονάδες είναι τα twips, και ένα pixel έχει πλάτος όσο το πλάτος.σημείου και ύψος όσο το ύψος.σημείου. Τα 1440 twips είναι μια λογική ίντσα στην οθόνη και μια κανονική στο χαρτί του εκτυπωτή. Η λογική ίντσα λέγεται έτσι γιατί ένα μόνιτορ μπορεί να αλλάζει το πραγματικό μήκος της, αλλά και η θέση μας από αυτήν αλλάζει το μέγεθος επίσης.

Το πρόγραμμα ρυθμίζει τα χρώματα φόντου και γραμμών/κειμένου, σε Ματζέντα και Κίτρινο.
Μπορούμε να δώσουμε html χρώματα όπου το #FF0000 είναι το κόκκινο, η με την Χρώμα(255, 0,0).

Επίσης ενεργοποιεί την χάραξη γραμμών με anti-aliasing μια διαδικασία που είναι αργότερη από την απλή χάραξη αλλά ομαλοποιεί τα σκαλοπάτια που δημιουργούν οι πλάγιες γραμμές.

Η Στη ή Let εδώ μπήκε για ομορφιά! Αν δεν την βάζαμε θα έπρεπε μεταξύ δυο εκχωρήσεων να βάλουμε την αλλαγή εντολής την άνω και κάτω τελεία και όχι το κόμμα.

Για να βγει το δένδρο στη μέση της οθόνης (όπως φαίνεται στην εικόνα παρακάτω) κάνουμε μερικούς υπολογισμούς για το πρώτο δένδρο και κατόπιν το καλούμε.

ΤΜΗΜΑ Δένδρο_Πυθαγόρα {
 ΟΘΟΝΗ 5, 0  ' ΜΑΤΖΕΝΤΑ, ΧΩΡΙΣ ΧΩΡΙΣΤΗ ΟΘΟΝΗ
 ΠΕΝΑ 14   ' ΚΙΤΡΙΝΟ
 ΟΜΑΛΑ ΝΑΙ  ' χρήση GDI+ για ομαλοποίηση στις γραμμές
 
 ΣΤΗ π =Χ.ΣΗΜΕΙΑ , υ = π * 11 ΔΙΑ 16
 ΣΤΗ π2 = π ΔΙΑ 2, διαφορά = π ΔΙΑ 12
 ΣΤΗ ΤάξηΔένδρου = 6
 Δένδρο_Πυθαγόρα(π2 - διαφορά, υ-10, π2 + διαφορά, υ-10, 0)
 
 ΡΟΥΤΙΝΑ Δένδρο_Πυθαγόρα(χ1, ψ1, χ2, ψ2, βάθος)
 
     ΑΝ βάθος > ΤάξηΔένδρου ΤΟΤΕ ΕΞΟΔΟΣ ΡΟΥΤΙΝΑΣ
 
     ΤΟΠΙΚΗ δχ = χ2 - χ1, δψ = ψ1 - ψ2
     ΤΟΠΙΚΗ χ3 = χ2 - δψ, ψ3 = ψ2 - δχ
     ΤΟΠΙΚΗ χ4 = χ1 - δψ, ψ4 = ψ1 - δχ
     ΤΟΠΙΚΗ χ5 = χ4 + (δχ - δψ) / 2
     ΤΟΠΙΚΗ ψ5 = ψ4 - (δχ + δψ) / 2
     ΘΕΣΗ χ1, ψ1
     ΧΑΡΑΞΕ ΕΩΣ χ2, ψ2
     ΧΑΡΑΞΕ ΕΩΣ χ3, ψ3
     ΧΑΡΑΞΕ ΕΩΣ χ4, ψ4
     ΧΑΡΑΞΕ ΕΩΣ χ1, ψ1
     Δένδρο_Πυθαγόρα(χ4, ψ4, χ5, ψ5, βάθος+1)
     Δένδρο_Πυθαγόρα(χ5, ψ5, χ3, ψ3, βάθος+1)
 
 ΤΕΛΟΣ ΡΟΥΤΙΝΑΣ
}
Δένδρο_Πυθαγόρα

Παραλλαγή του προγράμματος με χρήση τμήματος αντί για ρουτίνα.
Τα τμήματα είναι πιο βαριές κατασκευές από τις ρουτίνες.

Για να καλέσουμε ένα τμήμα πρέπει να έχει δοθεί από πριν ο ορισμός του. Επίσης για να καλέσουμε ένα τμήμα με αναδρομή πρέπει να χρησιμοποιήσουμε τη ΚΑΛΕΣΕ,

Εδώ έχουμε το εσωτερικό τμήμα με το ίδιο όνομα με το εξωτερικό. Η πρώτη κλήση καλεί το εσωτερικό και η δεύτερη επειδή είναι με την ΚΑΛΕΣΕ καλεί το τρέχον.

Δείτε τις αλλαγές:
1. Το έξοδος δεν έχει τη λέξη ΡΟΥΤΙΝΑΣ
2. Οι μεταβλητές που θέλουμε να διαβάζονται σε κάθε κλήση αναδρομής πρέπει να είναι γενικές, γιατί εντός τμήματος θέαση υπάρχει μόνο για τοπικές του τμήματος και γενικές.

Οι γενικές που φτιάχτηκαν σε ένα τμήμα διαγράφονται στο πέρας εκτέλεσης αυτού. Αν καλούσαμε ένα τμήμα μέσα από αυτό που φτιάξαμε μια γενική έστω Α και σε αυτό φτιάξουμε μια νέα γενική Α τότε η δεύτερη θα ισχύει μέχρι το τμήμα που τη δημιούργησε τερματίσει και στην επιστροφή η γενική Α θα υπάρχει με την τιμή που φτιάχτηκε στο πρώτο τμήμα. Με αυτό το τρόπο "σκίασης" μεταβλητών μπορούμε να έχουμε τμήματα με γενικές μεταβλητές δικές του χωρίς να ενοχλεί υπάρχουσες γενικές. Επίσης για να αλλάξουμε τιμή σε μια γενική έχουμε το <= και όχι το =. Αν υπάρχει γενική Β και σε ένα τμήμα δώσουμε το Β=100 τότε η γενική σκιάζεται με τη τοπική Β. Οι τοπικές σκιάζουν τις γενικές και νεότερες γενικές σκιάζουν υπάρχουσες γενικές (όταν έχουμε ίδιο όνομα σε κάθε περίπτωση).


Οι κλήσεις τμημάτων περιορίζονται σε βάθος σε μερικές χιλιάδες. Σε αντίθεση η κλήση ρουτινών μπορεί να είναι σε βάθος σε εκατοντάδες χιλιάδες.

ΤΜΗΜΑ Δένδρο_Πυθαγόρα {
 ΟΘΟΝΗ 5, 0  ' ΜΑΤΖΕΝΤΑ, ΧΩΡΙΣ ΧΩΡΙΣΤΗ ΟΘΟΝΗ
 ΠΕΝΑ 14   ' ΚΙΤΡΙΝΟ
 ΟΜΑΛΑ ΝΑΙ  ' χρήση GDI+ για ομαλοποίηση στις γραμμές
 
 ΓΕΝΙΚΕΣ π =Χ.ΣΗΜΕΙΑ , υ = π * 11 ΔΙΑ 16
 ΓΕΝΙΚΕΣ π2 = π ΔΙΑ 2, διαφορά = π ΔΙΑ 12
 ΓΕΝΙΚΕΣ ΤάξηΔένδρου = 6
 ΤΜΗΜΑ Δένδρο_Πυθαγόρα(χ1, ψ1, χ2, ψ2, βάθος) {
 
     ΑΝ βάθος > ΤάξηΔένδρου ΤΟΤΕ ΕΞΟΔΟΣ
 
     ΣΤΗ δχ = χ2 - χ1, δψ = ψ1 - ψ2
     ΣΤΗ χ3 = χ2 - δψ, ψ3 = ψ2 - δχ
     ΣΤΗ χ4 = χ1 - δψ, ψ4 = ψ1 - δχ
     ΣΤΗ χ5 = χ4 + (δχ - δψ) / 2
     ΣΤΗ ψ5 = ψ4 - (δχ + δψ) / 2
     ΘΕΣΗ χ1, ψ1
     ΧΑΡΑΞΕ ΕΩΣ χ2, ψ2
     ΧΑΡΑΞΕ ΕΩΣ χ3, ψ3
     ΧΑΡΑΞΕ ΕΩΣ χ4, ψ4
     ΧΑΡΑΞΕ ΕΩΣ χ1, ψ1
     ΚΑΛΕΣΕ Δένδρο_Πυθαγόρα χ4, ψ4, χ5, ψ5, βάθος+1
     ΚΑΛΕΣΕ Δένδρο_Πυθαγόρα χ5, ψ5, χ3, ψ3, βάθος+1
 }
 Δένδρο_Πυθαγόρα π2 - διαφορά, υ-10, π2 + διαφορά, υ-10, 0
}
Δένδρο_Πυθαγόρα

Στο Info αρχείο που υπάρχει στην εγκατάσταση της γλώσσας υπάρχει το Pyth με αγγλικές εντολές το πρώτο πρόγραμμα καθώς και το Pyth1 επίσης με αγγλικές εντολές με εμφάνιση δυο δένδρων υπό γωνία το ένα αντικριστό από το άλλο:

Pyth1:

MODULE Pythagoras_Example{
 CLS 5, 0  ' MAGENTA, split line = 0  
 PEN 14  ' YELLOW
 \\ Linux smoothing not work (we can use the statement but without effect)
 IF ISWINE ELSE SMOOTH ON
 \\ PYTHAGORAS TREE
 \\ by definition all variables ar type of a double
 GLOBAL p=7, p4=PI/4, p2=PI/2, s2=SQRT(2)/2
 MODULE center_p (r, t){
  MODULE pythagoras_tree (r, dx, depth) {
   r2=r-p2
   DRAW ANGLE r, dx
   DRAW ANGLE r2, dx
   DRAW ANGLE r, -dx
   DRAW ANGLE r2, -dx
   IF depth>10 THEN EXIT
   s3=dx*s2
   depth++
   STEP ANGLE r+p4, s3*2
   CALL pythagoras_tree r-p4,  s3, depth
   STEP ANGLE r, -dx-s3
   STEP ANGLE r, s3
   STEP ANGLE r+p4, -s3
   CALL pythagoras_tree r+p4,  s3, depth
   STEP ANGLE r-p4, s3  
  } 
  MOVE SCALE.X/2, SCALE.Y/2 
  STEP ANGLE PI-p4+r, t*s2
  CALL pythagoras_tree r, t, 1
 }
 r=PI/3
 pixels=100
 center_p r, 100*TWIPSX
 center_p r+PI, 100*TWIPSX
 CopyImageToClipboard()
 
 Sub CopyImageToClipboard()
  LOCAL Scr$=""
  MOVE 0,0
  COPY SCALE.X, SCALE.Y TO Scr$
  CLIPBOARD Scr$
 END SUB
}
Pythagoras_Example

Revision 9 Version 9.9

A bug from Print statement removed. From a version of Print, a Print @-2, ""; which send to channel -2 (to screen) the same way as send characters to a file. (can be use for text art).

Νέο μικρό εγχειρίδιο της Μ2000

Ανέβηκε το ανανεωμένο μικρό εγχειρίδιο που καλύπτει τρέχουσα έκδοση 9.9 αναθεώρηση 8.

Αναθεώρηση 8 Έκδοση 9.9

Μια διόρθωση στην Union.Data$() ή Ένωση.Σειράς$() για να δέχεται κωδικούς χαρακτήρων πάνω από 65535 (γράφονται σε 32bit, με δυο surrogates - που μπορούν να κρατήσουν μέχρι 20bit αριθμό).