Μια κρουαζιέρα στο ποτάμι (πρόταση στον κ. Περικλή Γεωργιάδη)

Είδα ένα βίντεο με τίτλο:

Μια κρουαζιέρα στο ποτάμι: από την αναλυτική επίλυση προβλήματος στην Υπολογιστική Σκέψη (CIE2020)

Εξηγεί πως ένα πρόβλημα υπολογιστικό μπορεί να λυθεί με "μαθηματικά". Αλλά στην ουσία μας δίνει τύπους μυστήριους που απαιτεί ρίζες, διακρίνουσες, τριώνυμα και "παπάδες".

Όμως αυτό δεν είναι Υπολογιστική Σκέψη, είναι Μαθηματική Σκέψη. Οπότε του δίνω μια πρόταση περί υπολογιστικής σκέψης για το πρόβλημα (με ανάλυση του προβήματος κατά τον προγραμματιστή). Δυστυχώς στο βίντεο δεν δίνει δικαίωμα να γράψει κανείς σχόλια, οπότε τα γράφω εδώ!

Δείτε το πρόβλημα με απλά λόγια και δείτε πως δουλεύει η υπολογιστική σκέψη!

Ένα κρουαζιερόπλοιο κάνει μια διαδρομή έστω 2 μιλίων, να πάει και να γυρίσει για έναν προορισμό! Η μισή διαδρομή, δ είναι κόντρα στο ρεύμα που έχει μια ταχύτητα ρ, έστω μισό μίλι την ώρα. Και στο πήγαινε και στο έλα η ταχύτητα του ρεύματος δεν αλλάζει. Ο καπετάνιος θέλει να ξέρει με τι ταχύτητα θα πρέπει να πηγαίνει για να καλύψει τη διαδρομή σε μια ώρα. Προφανώς αν έχει ταχύτητα 2 μίλια την ώρα δεν θα φτάσει σε μια ώρα γιατί το ρεύμα του αλλάζει τις συνθήκες.

Δείτε πως λύθηκε το πρόβλημα με ένα απλό προγραμμα!

Τεμαχίζουμε το χρόνο σε κβάντα, έστω 1000. Οπότε ένα κβάντο είναι ένα δτ, που είναι ίσο με τ/κβάντα. Πολλαπλασιάζουμε την ταχύτητα ρεύματος ρ με δτ και παίρνουμε το δρ, το διάστημα ανά δτ που θα κόβει ή θα δίνει στη πορεία μας. Υπολογίζουμε μια αρχική τιμή διαστήματος ανά δτ. Αν δεν είχαμε το ρεύμα θα ήταν 2*δ/τ  ή με αριθμούς 2*δ=2*1=2 μίλια ανά 1 ώρα, ή 2 μίλια την ώρα. Με ταχύτητα ρεύματος 0,5 μίλια την ώρα αν η διαδρομή ήταν όλη κόντρα στο ρεύμα θα θέλαμε 2,5 μίλια την ώρα για να κάνουμε 2,5-0.5 μίλια, δηλαδή τα 2 μίλια που θέλουμε. Τώρα για να είμαστε σε ένα καλό σημείο αρχικής ταχύτητας θα πούμε ότι η ταχύτητα δεν μπορεί να είναι μεγαλύτερη από το 120%, δηλαδή 2*120/100 ή 2,4 μίλια την ώρα (αφού θα είναι σίγουρα μικρότερη από 2,5 μίλια). Βρίσκουμε ένα δα που είναι η ταχύτητα δια το δτ, δηλαδή το δα είναι το διάστημα που θα καλύπτουμε ανά δτ λόγω της πρόωσης του πλοίου.

Το πρόβλημα ανάγεται σε μια επανάληψη όπου υπολογίζουμε τα κβάντα ως συνολικά κβάντα από τις δυο διαδρομές και τα συγκρίνουμε με τον αριθμό των αρχικών κβάντων (όπου όλα μαζί είναι το τ που θέλουμε). Ξέρουμε ότι το δα είναι μεγάλο και πρέπει να το μικραίνουμε διαδοχικά. Τώρα δεν μας ενδιαφέρει πόσο, θα το σκεφτούμε μετά! Μπορούμε να δοκιμάσουμε με τιμές όπως 0.001 ή κάτι άλλο!

Σεκφτόμαστε ότι σε μια κατεύθυνση στο δα θα προσθέτουμε το δρ και στην άλλη θα το αφαιρούμε. Οπότε λέμε ότι έχουμε μια πρόωση1 κατά δα+ρα και μια πρόωση2 κατά δα-ρα. 

Εδώ είναι το ζουμί, οι προώσεις είναι ανά δτ. Οπότε το δ/πρόωση1 είναι ο αριθμός των δτ ανά πρόωση1 για διάστημα δ. Ομοίως το δ/πρόωση2 είναι ο αριθμός των δτ ανά πρόωση2 για διάστημα δ. Προσθέτουμε τα δ/πρόωση1 και δ/πρόωση2 και έχουμε τον συνολικό αριθμό των δτ. Αν αυτός ο αριθμός είναι όσο ο αριθμός των κβάντων τότε έχουμε το σωστό δα, άρα η ταχύτητα είναι δα/δτ, αν όχι πρέπει να "μαγειρέψουμε" το δα, να το μικρύνουμε και να λογαριάσουμε πόσα συνολικά δτ μας δίνει.

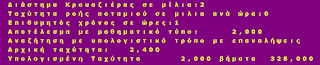
Το μαγείρεμα γίνεται εδώ με την εντολή δα-=επιπλέον+επιπλέον*Κβάντα/ΣυνολικάΚβάντα, όπου αφαιρούμε (δείτε το -= τελεστή) το επιπλέον και ένα ακόμα σχετικό με το λόγο Κβάντα/ΣυνολικάΚβάντα. Δηλαδή αφαιρούμε από επιπλέον και κατιτίς ως σχεδόν 2*επιπλέον όταν φτάσουμε στη λύση. Δηλαδή επιταγχύνουμε όταν πάμε προς τη λύση και έτσι πετυχαίνουμε λιγότερα βήματα. Δείτε στη φωτογραφία ότι χρειάστηκαν 88 βήματα.

Εισαγωγή "Διάστημα Κρουαζιέρας σε μίλια:",δ2
δ=(δ2 δια 2)
Εισαγωγή "Ταχύτητα ροής ποταμιού σε μιλια ανά ώρα:",ρ
Εισαγωγή "Επιθυμητός χρόνος σε ώρες:", τ
Τύπωσε "Αποτέλεσμα με μαθηματικό τύπο:", (δ+ριζα(δ**2+τ**2*ρ**2))/τ
Τύπωσε "Αναζήτηση με υπολογιστικό τρόπο με επαναλήψεις"
Κβάντα=1000
δτ=τ/Κβάντα
δρ=ρ*δτ
δα=(2*δ/τ*120/100)*δτ
Τύπωσε $("0.000"), "Αρχική ταχύτητα:", δα/δτ
επιπλέον=δα/κβάντα/10
βήματα=0
ΣυνολικάΚβάντα=1
Ενώ  ΣυνολικάΚβάντα<Κβάντα
	δα-=επιπλέον+επιπλέον*Κβάντα/ΣυνολικάΚβάντα
	πρόωση1=δα+δρ  ' ανά δτ
	πρόωση2=δα-δρ  ' ανά δτ
	ΣυνολικάΚβάντα=δ/πρόωση1+ δ/πρόωση2
	βήματα++
Τέλος Ενώ
Τύπωσε "Υπολογισμένη Ταχύτητα", δα/δτ, " βήματα", βήματα

Συμπέρασμα:

Η υπολογιστική σκέψη, μένει στα φαινόμενα και δεν καταπιάνεται με μαθηματικά υψηλού επιπέδου όπως ορίζουσες, διπλές λύσεις κ.α.

Εδώ βοηθάει περισσότερο η Χημεία παρά τα Μαθηματικά και το εξηγώ. Στη χημεία τα "ποσοτικά" ζητήματα λύνονται υοθετόντας μια βάση, έστω 100 moles. Στο πρόβλημα παραπάνω η βάση μας είναι τα 1000 κβάντα. Το φαινόμενο που αλλάζει στο πήγαινε και στο έλα είναι το διάστημα ανά δτ, δηλαδή η ταχύτητα ανά δτ.

Σε όλα τα υπολογιστικά προγράμματα (γενικώς και σε όλα τα προγράμματα) μετράει τι βάζουμε ως αρχικές τιμές! Εδώ τι βάζουμε ως αρχική "ψεύτικη" ταχύτητα δα/δτ, ή διάστημα δα ανά δτ, ανά κβάντο χρόνου! Στο πρόγραμμα το κβάντο χρόνου το έχουμε σε αριθμό είναι το δτ, δηλαδή το τ/1000, με το 1000 να το επιλέγουμε Αυθαίρετα (έτσι λειτουργούμε και σε προβλήματα της Χημείας).

Δείτε τι βγάζει το πρόγραμμα αν δώσουμε ταχύτητα ροής 0. Έτσι ελέγχουμε αν είμαστε σωστοί! Επίσης δείτε ότι με επιλογή 2,40 αρχική ταχύτητα ήθελε 328 βήματα για να βρει τη σωστή. Αυτό συμβαίνει γιατί το 2,40 είναι κάπως μεγάλη τιμή για την περίπτωση! Την τιμή 2.40 ή 120% πάνω στην βασική τιμή την υπολογίσαμε χοντρικά για το 0.5 της ταχύτητας με υπόθεση ότι το μάξιμουμ θα ήταν 2,5, ενώ η τελική τιμή ήταν 2,112 (στρογγυλεμένη, στο τρίτο δεκαδικό).

Μια πιο γενικευμένη μορφή που αυτορυθμίζεται αν δει ότι βρήκε λύση πολύ γρήγορα (κάτω από δέκα βήματα)

Εισαγωγή "Διάστημα Κρουαζιέρας σε μίλια:",δ2
δ2=απολ(δ2)
δ=(δ2 δια 2)
Εισαγωγή "Ταχύτητα ροής ποταμιού σε μιλια ανά ώρα:",ρ
Εισαγωγή "Επιθυμητός χρόνος σε ώρες:", τ
τ=απολ(τ)
Τύπωσε "Αποτέλεσμα με μαθηματικό τύπο:", (δ+ριζα(δ**2+τ**2*ρ**2))/τ
Τύπωσε "Αναζήτηση με υπολογιστικό τρόπο με επαναλήψεις"
Αν ρ=0 τότε Κβάντα=300 αλλιώς Κβάντα=300*Οροφ(δ/ρ/100)
Τύπωσε "Κβάντα:", Κβάντα
δτ=τ/Κβάντα
δρ=ρ*δτ
δα=(δ2/τ+ρ)*δτ
Τύπωσε $("0.000"), "Αρχική ταχύτητα:", δα/δτ
επιπλέον=δα/κβάντα/(11*τ+1)
ξανά:
	βήματα=0
	ΣυνολικάΚβάντα=1
	Ενώ  ΣυνολικάΚβάντα<Κβάντα
		δα-=επιπλέον+επιπλέον*Κβάντα/ΣυνολικάΚβάντα
		πρόωση1=δα+δρ  ' ανά δτ
		πρόωση2=δα-δρ  ' ανά δτ
		ΣυνολικάΚβάντα=δ/πρόωση1+ δ/πρόωση2
		βήματα++
	Τέλος Ενώ
Αν βήματα<10 τότε δα=(δ2/τ+ρ)*δτ:επιπλέον/=10: Τύπωσε "Ρύθμιση": προς ξανά
Τύπωσε "Υπολογισμένη Ταχύτητα", δα/δτ, " βήματα", βήματα